머신러닝으로 단백질 용해도 예측하기
0. 단백질 용해도 예측¶
유전자 재조합을 통해 특정 단백질을 과발현시키는 것은 생명과학에서 아주 중요한 일입니다. 그러나 대부분의 과발현 단백질은 inclusion bodies를 형성해 용해도가 매우 낮은 문제가 있습니다. 그렇기 때문에 단백질 용해도를 예측하는 일은 실험의 시행착오를 줄이는데 도움이 됩니다.
여기서는 대장균에서 발현되는 단백질 데이터를 가지고 기계학습으로 용해도를 예측하는 문제를 풀어보겠습니다.
1. eSOL 데이터셋 설명¶
분석에 사용한 eSOL(Solubility database of all E.coli proteins) 데이터셋은 Targeted Proteins Research Project을 통해 http://tp-esol.genes.nig.ac.jp/ 에 공개 되어있습니다.
공식 페이지에서는 해당 데이터셋에 대해 다음과 같이 설명 합니다.
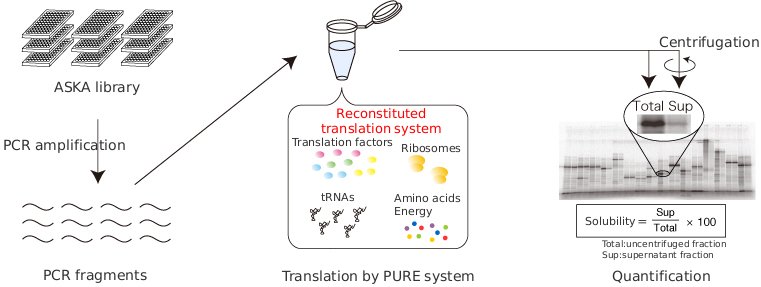
eSOL is a database on the solubility of entire ensemble E.coli proteins (Niwa T, Ying BW, Saito K, Jin W, Takada S, Ueda T and Taguchi H, 2009) individually synthesized by PURE system that is chaperone free.
대장균(E.coli) 단백질의 용해도(Solubility)는 아래의 공식을 통해 계산되었습니다.
$$ Solubility = \frac{Supernatant fraction}{uncentrifuged fraction} * 100 $$
따라서 주의해야 할 것은 용해도가 동일해도 전체 발현량은 동일하지 않을 수 있습니다.
2. 데이터셋 불러오기¶
pandas 라이브러리를 사용해 데이터셋을 불러옵니다. 원본 데이터셋은 tsv형식으로 되어 있지만, 편의를 위해 csv형식으로 변경하고 단백질 서열 정보를 추가했습니다.
In [1]:
import pandas as pd
df = pd.read_csv("E_coli_protein.csv")
df.tail()
Out[1]:
In [2]:
AA = [
"A",
"C",
"D",
"E",
"F",
"G",
"H",
"I",
"K",
"L",
"M",
"N",
"P",
"Q",
"R",
"S",
"T",
"V",
"W",
"Y",
]
for i in AA:
df[i] = [x.count(i) / len(x) for x in df["Sequence"]]
이제 Biopython 라이브러리에 있는 도구를 사용해 추가적인 데이터를 만들어 보겠습니다.
3.2. 단백질의 분자량¶
Biopython.ProteinAnalysis 객체를 사용합니다.
In [3]:
from Bio.SeqUtils.ProtParam import ProteinAnalysis
df["molecular_weight"] = [ProteinAnalysis(x).molecular_weight() for x in df["Sequence"]]
3.3. 다양한 계산값¶
단백질의 방향족(aromaticity) 아미노산 비율, 불안정성(instability index), 등전점(isoelectric point)등에 관한 값을 추가합니다.
In [4]:
df["aromaticity"] = [ProteinAnalysis(x).aromaticity() for x in df["Sequence"]]
df["instability_index"] = [
ProteinAnalysis(x).instability_index() for x in df["Sequence"]
]
df["isoelectric_point"] = [
ProteinAnalysis(x).isoelectric_point() for x in df["Sequence"]
]
df["gravy"] = [ProteinAnalysis(x).gravy() for x in df["Sequence"]]
3.4. 단백질 2차 구조¶
단백질 2차 구조의 비율에 대한 값을 추가합니다. 현재 단백질 서열을 통해 2차 구조를 예측하는 것은 상당히 정확한 편입니다.
In [5]:
df["structure_fraction_helix"] = [
ProteinAnalysis(x).secondary_structure_fraction()[0] for x in df["Sequence"]
]
df["structure_fraction_turn"] = [
ProteinAnalysis(x).secondary_structure_fraction()[1] for x in df["Sequence"]
]
df["structure_fraction_sheet"] = [
ProteinAnalysis(x).secondary_structure_fraction()[2] for x in df["Sequence"]
]
3.5. 흡광 계수¶
단백질의 흡광 계수는 주로 농도를 계산하는데 사용되는 값으로 소수성 아미노산과 시스테인(cysteine)의 비율과 관련있습니다.
In [6]:
df["extinction_coefficient_reduced"] = [
ProteinAnalysis(x).molar_extinction_coefficient()[0] for x in df["Sequence"]
]
df["extinction_coefficient_non_reduced"] = [
ProteinAnalysis(x).molar_extinction_coefficient()[1] for x in df["Sequence"]
]
3.6. 단백질 유연성 정보¶
단백질 서열의 각 위치에 대한 아미노산 유연성을 계산합니다. 그런다음 평균값과 표준편차, 중간값을 추가합니다.
In [8]:
import numpy as np
df["flexibility_mean"] = [
np.mean(ProteinAnalysis(x).flexibility()) for x in df["Sequence"]
]
df["flexibility_std"] = [
np.std(ProteinAnalysis(x).flexibility()) for x in df["Sequence"]
]
df["flexibility_median"] = [
np.median(ProteinAnalysis(x).flexibility()) for x in df["Sequence"]
]
각 아미노산의 유연성에 대한 조화평균, 기하평균, 최소값, 최대값, 왜도, 첨도값을 추가합니다.
In [10]:
from scipy.stats.mstats import hmean, gmean
from scipy.stats import skew, kurtosis
df["flexibility_hmean"] = [
hmean(ProteinAnalysis(x).flexibility()) for x in df["Sequence"]
]
df["flexibility_gmean"] = [
gmean(ProteinAnalysis(x).flexibility()) for x in df["Sequence"]
]
df["flexibility_min"] = [
np.min(ProteinAnalysis(x).flexibility()) for x in df["Sequence"]
]
df["flexibility_max"] = [
np.max(ProteinAnalysis(x).flexibility()) for x in df["Sequence"]
]
df["flexibility_skew"] = [
skew(ProteinAnalysis(x).flexibility()) for x in df["Sequence"]
]
df["flexibility_kurtosis"] = [
kurtosis(ProteinAnalysis(x).flexibility()) for x in df["Sequence"]
]
추가한 데이터를 확인해 봅니다.
In [12]:
df.tail()
Out[12]:
원래 4개의 행으로 구성되어 있던 데이터셋에 39개의 행이 추가되어 총 43개 행을 갖게 되었습니다. 수치로 되어있는 행에 대한 산술 통계값을 살펴봅니다.
In [11]:
df.describe()
Out[11]:
위 테이블을 통해 용해도의 표준편차값이 높다는 것과 생성한 데이터들이 음수값도 포함하고 있다는 것을 알 수 있습니다.
3.7. 데이터 행 정렬¶
데이터 처리의 편의를 위해 Solubility, Sequence 행의 위치를 변경합니다.
In [13]:
df.columns.values
Out[13]:
In [14]:
column_titles = [
"Number",
"Gene",
"A",
"C",
"D",
"E",
"F",
"G",
"H",
"I",
"K",
"L",
"M",
"N",
"P",
"Q",
"R",
"S",
"T",
"V",
"W",
"Y",
"molecular_weight",
"aromaticity",
"instability_index",
"isoelectric_point",
"structure_fraction_helix",
"structure_fraction_turn",
"structure_fraction_sheet",
"extinction_coefficient_reduced",
"extinction_coefficient_non_reduced",
"gravy",
"flexibility_mean",
"flexibility_std",
"flexibility_median",
"flexibility_hmean",
"flexibility_gmean",
"flexibility_min",
"flexibility_max",
"flexibility_skew",
"flexibility_kurtosis",
"Sequence",
"Solubility",
]
df = df.reindex(columns=column_titles)
In [15]:
df.tail()
Out[15]:
3.8. 데이터셋 파일로 저장¶
아래 명령어를 통해 데이터셋을 파일로 저장 할 수 있습니다.
In [16]:
# df.to_csv("Engineered_E_coli_protein.csv", mode='w', index=False)
In [17]:
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
sns.scatterplot(
y="Solubility",
x="molecular_weight",
linewidth=0.1,
alpha=0.5,
sizes=(1, 8),
data=df,
)
Out[17]:
이미 알려져있는것 처럼 단백질의 크기가 클수록 용해도가 낮다는 것을 시각화를 통해 확인할 수 있습니다. 그러나 Scatter plot에는 겹쳐진 데이터가 너무 많기때문에 더 보기 좋은 그림을 그려봅니다.
4.2. Kernel density estimation plot¶
In [18]:
sns.jointplot(x="molecular_weight", y="Solubility", data=df, kind="kde")
Out[18]:
위 시각화를 통해 대부분의 단백질의 크기는 30kDa 주변에 몰려있으며, 용해도는 20%와 80% 그룹으로 나뉜다는 것을 알 수 있습니다. 또한 상대적으로 높은 용해도의 단백질은 25kDa 이하의 크기입니다.
5. 데이터 전처리¶
기계학습을 위해 데이터셋을 특성(feature)값과 결과값으로 분리합니다.
In [19]:
df_y = df["Solubility"]
df_x = df.iloc[:, 2:-2]
df_x.columns
Out[19]:
5.1. 특성값 정규화하기¶
정규화를 통해 기계 학습 모델이 특정 특성값에 바이어스(Bias)를 갖지 않게 합니다.
In [20]:
from sklearn import preprocessing
from sklearn.model_selection import train_test_split
scaler = preprocessing.StandardScaler().fit(df_x)
X_scaled = scaler.transform(df_x)
X_train, X_test, y_train, y_test = train_test_split(
X_scaled, df_y, test_size=0.2, random_state=42
)
In [21]:
from sklearn.linear_model import LinearRegression
import numpy as np
lin_reg = LinearRegression(n_jobs=-1) # -1 means use all cpu core
lin_reg.fit(X_train, y_train)
Out[21]:
In [23]:
from sklearn.metrics import mean_absolute_error
def evaluate(model, X_test, y_test):
y_pred = model.predict(X_test)
mape = mean_absolute_error(y_test, y_pred)
accuracy = 100 - mape
return accuracy
accuracy = evaluate(lin_reg, X_test, y_test)
print(f"Accuracy = {accuracy:.2f} %")
선형모델을 사용했을때 예측의 정확도는 약 77% 입니다.
In [24]:
from sklearn.tree import DecisionTreeRegressor
tree_reg = DecisionTreeRegressor()
tree_reg.fit(X_train, y_train)
accuracy = evaluate(tree_reg, X_test, y_test)
print(f"Accuracy = {accuracy:.2f} %")
In [25]:
from sklearn.svm import SVR
svm_reg = SVR(kernel="linear")
svm_reg.fit(X_train, y_train)
accuracy = evaluate(svm_reg, X_test, y_test)
print(f"Accuracy = {accuracy:.2f} %")
In [26]:
from sklearn.ensemble import RandomForestRegressor
forest_reg = RandomForestRegressor(n_estimators=1000, n_jobs=-1)
forest_reg.fit(X_train, y_train)
accuracy = evaluate(forest_reg, X_test, y_test)
print(f"Accuracy = {accuracy:.2f} %")
In [27]:
from sklearn.ensemble import GradientBoostingRegressor
gbr = GradientBoostingRegressor()
gbr.fit(X_train, y_train)
accuracy = evaluate(gbr, X_test, y_test)
print(f"Accuracy = {accuracy:.2f} %")
# print(f'Score = {gbr.score(X_train, y_train)}') # R^2 socre
In [28]:
# explicitly require this experimental feature
from sklearn.ensemble import HistGradientBoostingRegressor
hgr = HistGradientBoostingRegressor()
hgr.fit(X_train, y_train)
accuracy = evaluate(hgr, X_test, y_test)
print(f"Accuracy = {accuracy:.2f} %")
# print(f'Score = {hgr.score(X_train, y_train)}') # R^2 socre
가장 최근에 추가된 기능인 HistGradientBoostingRegressor이 가장 좋은 성능을 보여줍니다.
6.2. 특성의 중요도¶
이제 데이터의 어느 특성이 모델 예측에 중요한지 살펴보겠습니다. 간단한 시각화로 막대그래프를 그려봅니다.
In [40]:
feature_importances = gbr.feature_importances_
plt.bar(range(len(feature_importances)), feature_importances)
Out[40]:
위 그림을 통해 예측에 영향을 주는 특성을 알 수 있습니다. 상위 3가지를 알아보면 다음과 같습니다.
- 분자량(21번째 특성)
- pI값(29번째 특성)
- 분광계수(24번째 특성)
7. 모델의 매개 변수 최적화¶
GridSearchCV를 사용해 가장 좋은 성능을 나타내는 매개변수 값을 찾아봅니다.
In [35]:
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import make_scorer
def evaluate(y_true, y_pred):
mape = mean_absolute_error(y_true, y_pred)
accuracy = 100 - mape
return accuracy
score = make_scorer(evaluate, greater_is_better=True)
param_grid = [
{
"learning_rate": [0.01, 0.1],
"max_depth": [10, 50, 100],
"min_samples_leaf": [10, 50, 100],
}
]
hgr_reg = HistGradientBoostingRegressor(random_state=42)
grid_search = GridSearchCV(hgr_reg, param_grid, cv=5, scoring=score, n_jobs=-1)
grid_search.fit(X_train, y_train)
Out[35]:
In [36]:
cvres = grid_search.cv_results_
for mean_score, params in zip(cvres["mean_test_score"], cvres["params"]):
print(f"Score = {mean_score:.2f}, Params = {params} ")
최고의 성능을 보인 모델의 정확도는 아래와 같습니다.
In [37]:
grid_search.best_score_
Out[37]:
매개변수 값이 아래와 같을때 최고의 성능을 보여주었습니다.
In [38]:
grid_search.best_params_
Out[38]:
8. 마치며¶
생성한 기계 학습 모델에 임의의 단백질 서열을 넣어 용해도를 예측해보겠습니다. 임의의 서열 2가지를 csv파일에 넣어 데이터 전처리과정을 동일하게 거칩니다.
In [42]:
df2 = pd.read_csv("sol_predict.csv")
df2
Out[42]:
In [43]:
def feature_eng(df):
for i in AA:
df[i] = [x.count(i) / len(x) for x in df["Sequence"]]
df["molecular_weight"] = [
ProteinAnalysis(x).molecular_weight() for x in df["Sequence"]
]
df["aromaticity"] = [ProteinAnalysis(x).aromaticity() for x in df["Sequence"]]
df["instability_index"] = [
ProteinAnalysis(x).instability_index() for x in df["Sequence"]
]
df["isoelectric_point"] = [
ProteinAnalysis(x).isoelectric_point() for x in df["Sequence"]
]
df["gravy"] = [ProteinAnalysis(x).gravy() for x in df["Sequence"]]
df["structure_fraction_helix"] = [
ProteinAnalysis(x).secondary_structure_fraction()[0] for x in df["Sequence"]
]
df["structure_fraction_turn"] = [
ProteinAnalysis(x).secondary_structure_fraction()[1] for x in df["Sequence"]
]
df["structure_fraction_sheet"] = [
ProteinAnalysis(x).secondary_structure_fraction()[2] for x in df["Sequence"]
]
df["extinction_coefficient_reduced"] = [
ProteinAnalysis(x).molar_extinction_coefficient()[0] for x in df["Sequence"]
]
df["extinction_coefficient_non_reduced"] = [
ProteinAnalysis(x).molar_extinction_coefficient()[1] for x in df["Sequence"]
]
df["flexibility_mean"] = [
np.mean(ProteinAnalysis(x).flexibility()) for x in df["Sequence"]
]
df["flexibility_std"] = [
np.std(ProteinAnalysis(x).flexibility()) for x in df["Sequence"]
]
df["flexibility_median"] = [
np.median(ProteinAnalysis(x).flexibility()) for x in df["Sequence"]
]
df["flexibility_hmean"] = [
hmean(ProteinAnalysis(x).flexibility()) for x in df["Sequence"]
]
df["flexibility_gmean"] = [
gmean(ProteinAnalysis(x).flexibility()) for x in df["Sequence"]
]
df["flexibility_min"] = [
np.min(ProteinAnalysis(x).flexibility()) for x in df["Sequence"]
]
df["flexibility_max"] = [
np.max(ProteinAnalysis(x).flexibility()) for x in df["Sequence"]
]
df["flexibility_skew"] = [
skew(ProteinAnalysis(x).flexibility()) for x in df["Sequence"]
]
df["flexibility_kurtosis"] = [
kurtosis(ProteinAnalysis(x).flexibility()) for x in df["Sequence"]
]
return df
df2 = feature_eng(df2)
df2
Out[43]:
In [49]:
column_titles = [
"Number",
"Gene",
"A",
"C",
"D",
"E",
"F",
"G",
"H",
"I",
"K",
"L",
"M",
"N",
"P",
"Q",
"R",
"S",
"T",
"V",
"W",
"Y",
"molecular_weight",
"aromaticity",
"instability_index",
"isoelectric_point",
"structure_fraction_helix",
"structure_fraction_turn",
"structure_fraction_sheet",
"extinction_coefficient_reduced",
"extinction_coefficient_non_reduced",
"gravy",
"flexibility_mean",
"flexibility_std",
"flexibility_median",
"flexibility_hmean",
"flexibility_gmean",
"flexibility_min",
"flexibility_max",
"flexibility_skew",
"flexibility_kurtosis",
"Sequence",
]
df2 = df2.reindex(columns=column_titles)
df_x2 = df2.iloc[:, 2:-1]
X2_scaled = scaler.transform(df_x2)
이제 기계학습 모델을 사용해 용해도값을 예측해봅니다.
In [61]:
pred_sol = grid_search.best_estimator_.predict(X2_scaled)
gene = ["random", "DPO1_THEAQ"]
for idx, val in enumerate(gene):
print(f"Predicted solubility of {val} is {pred_sol[idx]:.2f}%")
위 코드를 통해 각각의 서열에 대한 용해도값을 예측 할 수 있었지만 실제값과 동일한지는 실제 실험을 해봐야할 것입니다.