파이썬으로 PK 분석하기
0. Pharmacokinetics(PK) 분석¶
ELISA를 이용하여 혈액에서 시험 약물의 약물학적 동태(Pharmacokinetics)를 평가한 데이터를 분석해보도록 하겠습니다. Pharmacokinetics(이하, PK)는 간단히 말하면 특정 약물에 대해서 몸이 어떻게 반응하는지를 보는 것입니다.
Pharmacokinetics은 약물의 흡수, 분포, 대사, 배설과정을 동역학적 관점에서 해석하고 예측하고자 하는 것이다. -- 위키백과
PK 분석을 통해서 약물의 반감기를 분석하고 약물 주입방식에 따른 차이를 살펴보도록 하겠습니다.
0.1. 실험 디자인¶
실험 쥐에 약물 X를 아래의 두가지 주입방식으로 실험합니다. 정확도를 위해 3번 반복하여 값을 측정하였습니다.
- IV(intravenous injection): 정맥주사
- SC(subcutaneous injection): 피하주사
주입후 72시간동안 실험 쥐의 혈액을 채취해 남아있는 약물 X의 양을 구합니다.
1. 데이터 불러오기¶
필요한 라이브러리를 불러옵니다.
# load modules
%matplotlib inline
import matplotlib.pyplot as plt
import pandas as pd
실험 결과를 정리한 CSV파일을 pd.read_csv()를 이용해 읽어옵니다.
# read csv file to analysis
df = pd.read_csv("./data/20180108_PK.csv")
num = df._get_numeric_data() # 음수 값을 0으로
num[num < 0] = 0
df.sample(5)
2. 데이터 전처리¶
Injection 방법에 의한 차이와 샘플을 채취한 시간, 실험용 쥐의 번호등을 확인 할 수 있습니다. 데이터 전처리 과정에서 필요없는 행을 삭제하고 반복측정한 값의 평균값과 표준편차를 계산하겠습니다.
# 필요없는 행 삭제
df = df.drop(["Sample", "Wells", "Value", "R"], axis=1)
# Inject 종류에 따라서 데이터 분리
df_IV = df[df["Inject"] == "IV"]
df_SC = df[df["Inject"] == "SC"]
df_IV.head()
groupby()기능을 사용해 시간별로 그룹핑 합니다. 그런다음 평균값과 표준편차를 구합니다.
# 평균값
mean_IV = df_IV.groupby("Time(h)").mean()
mean_SC = df_SC.groupby("Time(h)").mean()
# 표준편차
std_IV = df_IV.groupby("Time(h)").std()
std_SC = df_SC.groupby("Time(h)").std()
mean_IV # IV 테이블을 확인합니다.
plt.plot(mean_IV["Result"], "o-") # IV 값
plt.plot(mean_SC["Result"], "o--") # SC 값
2.2. 선그래프에 에러바 추가하기¶
위의 그래프에서는 IV injection의 두번째 값이 좀 낮은 것 같은데, 표준편차가 표시되어 있지 않아 실제값 자체가 낮은 것인지 실험상의 편차인지 명확하지 않습니다. plt.errorbar()를 이용해서 에러바를 표시해 알아 보도록 하죠.
fig, ax = plt.subplots()
fig_name = "PK_analysis"
ax.set(title=fig_name, xlabel="Time(h)", ylabel="Activity(IU/ml)")
ax.errorbar(
x=mean_IV.index.values,
y=mean_IV["Result"],
yerr=std_IV["Result"],
fmt="o-",
capsize=3,
label="IV",
)
ax.errorbar(
x=mean_SC.index.values,
y=mean_SC["Result"],
yerr=std_SC["Result"],
fmt="o-",
capsize=3,
label="SC",
)
plt.legend() # 범례 표시
ax.spines["right"].set_visible(False) # 프레임 숨기기
ax.spines["top"].set_visible(False)
# plt.savefig(fig_name + '.png', dpi = 600 ) # 저장하기
IV injection의 두번째 값의 표준편차가 큰것을 확인할 수 있습니다. 따라서 실험상의 편차로 인해 나타난 현상이라고 볼 수 있겠습니다.
3. 반감기 계산¶
Pharmacokinetics 실험의 목적이라고 할 수 있는 약물의 반감기를 계산해 보도록 하겠습니다. 계산을 위해선 실험 데이터에 Curve fitting을 수행해야 합니다. 파이썬에서는 scipy.optimize.curve_fit() 을 사용하도록 하겠습니다.
# 필요한 라이브러리를 불러옵니다.
from scipy.optimize import curve_fit
import numpy as np
import warnings # 경고를 무시합니다.
warnings.filterwarnings("ignore")
전체적인 PK 데이터의 모양을 보면 가장 간단한 one-compartment model를 사용하면 될 것 같습니다. 먼저 지수(exponential) 함수를 정의해 Curve fitting을 합니다.
def exponential(x, D, k):
return D * np.exp(-k * x)
x = np.array(mean_IV.index.values)
y = np.array(mean_IV["Result"])
# curve fitting 하기
popt, pcov = curve_fit(exponential, x, y)
ss_res = np.sum((y - exponential(x, *popt)) ** 2) # residual sum of squares
ss_tot = np.sum((y - np.mean(y)) ** 2) # total sum of squares
r2 = 1 - (ss_res / ss_tot) # r-squared
print("R-squared is {:.3f}%.".format(r2 * 100))
# 시각화
xx = np.linspace(0, 80, 1000)
yy = exponential(xx, *popt)
plt.plot(x, y, "o")
plt.plot(xx, yy)
두번째 포인트 값이 역시나 말썽입니다. 전체적인 R2값도 낮습니다. 몇개의 값을 제외하고 다시 해보겠습니다.
# 2번째, 4번째 데이터를 제외
selection = np.array([0, 2, 3, 5, 6, 7])
x = x[selection]
y = y[selection]
# curve fitting 하기
popt, pcov = curve_fit(exponential, x, y)
ss_res = np.sum((y - exponential(x, *popt)) ** 2) # residual sum of squares
ss_tot = np.sum((y - np.mean(y)) ** 2) # total sum of squares
r2 = 1 - (ss_res / ss_tot) # r-squared
print("R-squared is {:.3f}%.".format(r2 * 100))
# 시각화
xx = np.linspace(0, 80, 1000)
yy = exponential(xx, *popt)
plt.plot(x, y, "o")
plt.plot(xx, yy)
아까보다는 좀 더 잘맞는 것 같습니다. 일단은 반감기를 구해보도록 하죠.
반감기 계산¶
반감기는 주입한 약물의 양이 1/2로 감소하는 데 소요되는 시간입니다. 반감기를 구하는 공식이 따로 있기는 합니다만, 여기서는 Curve fiiting에 사용한 함수의 역함수를 정의해서 주입한 약물양의 절반이 되는 시간을 구해보겠습니다.
half_y = exponential(0, *popt) / 2 # 주입한 약물량을 2로 나누어 줍니다
# 계산을 위한 역함수를 정의합니다.
def rev_log(y, D, k):
"""for halflife calculate"""
return (np.log(y) - np.log(D)) / -k
half_life = rev_log(half_y, *popt)
print("반감기는 {:.2f} 시간 입니다.".format(half_life))
# print(0.693/popt[1]) # Equation 에 의해 계산되는 값
x = np.array(mean_SC.index.values)
y = np.array(mean_SC["Result"])
x = x[3:]
y = y[3:]
# curve fitting 하기
popt, pcov = curve_fit(exponential, x, y)
ss_res = np.sum((y - exponential(x, *popt)) ** 2) # residual sum of squares
ss_tot = np.sum((y - np.mean(y)) ** 2) # total sum of squares
r2 = 1 - (ss_res / ss_tot) # r-squared
print("R-squared is {:.3f}%.".format(r2 * 100))
# 시각화
xx = np.linspace(16, 80, 1000)
yy = exponential(xx, *popt)
plt.plot(x, y, "o")
plt.plot(xx, yy)
반감기 계산¶
half_y = exponential(16, *popt) / 2 # 주입한 약물량을 2로 나누어 줍니다
# 계산을 위한 역함수를 정의합니다.
def rev_log(y, D, k):
"""for halflife calculate"""
return (np.log(y) - np.log(D)) / -k
half_life = rev_log(half_y, *popt)
print("반감기는 {:.2f} 시간 입니다.".format(half_life))
4. Bioavailability(BA) 계산¶
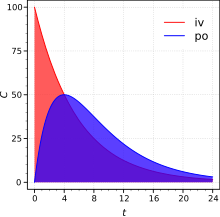
약물의 흡수는 생체 이용률(bioavailability)로 나타내는데, 경구로 투여된 약물이 전신순환계에 들어가 생체에 이용되는 비율을 말하며, 투여 후 혈중 약물 농도의 총 면적, 즉 AUC(Area Under the Concentration- time Curve)가 생체 이용률의 지표로 흔히 쓰이고 있다. -- Kyung Soo Kim, et al. Drug Effect and Generic Substitution
4.1. The absolute bioavailability¶
정맥투여에 대한 상대적인 흡수율을 나타내며, %로 표시하기에 절대적 생체 이용률이라고 한다. 약 물을 정맥에 투여할 때에는 곧 바로 전신순환에 도달되기 때문에 전신약물 흡수 즉 생체 이용률은 100%으로 생각한다. -- Kyung Soo Kim, et al. Drug Effect and Generic Substitution
아래의 공식은 절대적 생체 이용률(BA)를 구하는 방법입니다.
- po = Oral route; 경구투여
- iv = Intravenous injection; 정맥주사
- D = Dose; 투여량
이번 예시에서는 경구투여대신 SC(피하주사) 데이터를 사용해 절대 생체 이용률을 구해 보겠습니다. 파이썬에서는 sklearn.metrics() 기능을 사용해 손쉽게 그래프의 AUC를 구할 수 있습니다. 각각의 AUC를 구해서 상대적 비교를 하면 BA를 계산할 수 있습니다.
from sklearn import metrics # 필요한 라이브러리 불러오기
x1 = np.array(mean_IV.index.values)
y1 = np.array(mean_IV["Result"])
x2 = np.array(mean_SC.index.values)
y2 = np.array(mean_SC["Result"])
# 각각의 AUC를 구합니다.
IV_auc = metrics.auc(x1, y1)
SC_auc = metrics.auc(x2, y2)
IV_conc = 100
SC_conc = 50
# 수식에 맞춰 BA를 계산합니다.
BA = (SC_auc * IV_conc) / (IV_auc * SC_conc)
print("Bioavailability of SC injection is {:.2f}%.".format(BA * 100))
5. 마치며¶
이번 포스트에서는 파이썬을 이용해 간단한 PK 분석을 해보았습니다. 저도 이쪽의 전문가가 아니라 직접 찾아보며 계산했습니다. 틀린 부분이 있다면 이해해주시기 바랍니다. 약물의 반감기와 BA는 다양한 PK 변수중에 극히 일부이지만, 이러한 변수를 구하는 방법을 안다면 다른 변수들도 쉽게 계산할 수 있으실 것입니다.

